Dalam ekonomi terdapat permintaan dan penawaran yang saling bertemu dan membentuk satu titik pertemuan dalam satuan harga dan kuantitas (jumlah barang). Setiap transaksi perdagangan pasti ada permintaan, penawaran, harga dan kuantitas yang saling mempengaruhi satu sama lain.
Pengertian Permintaan
Permintaan adalah sejumlah barang yang dibeli atau diminta di dalam suatu harga dan sewaktu tertentu. Permintaan berkaitan dengan keinginan konsumen akan sebuah barang dan jasa yang ingin dipenuhi. Dan kecenderungan permintaan konsumen akan barang dan jasa tak terbatas.
Hukum Permintaan
Hukum permintaan adalah hukum yang menerangkan tentang adanya hubungan yang bersifat negatif antara fase harga dengan jumlah barang yang diminta. Apabila dan naik jumlah barang yang diminta sedikit dan jika harga rendah jumlah barang yang diminta meningkat
Dengan demikian hukum permintaan berbunyi :
“Semakin turun tingkat harga, maka semakin banyak jumlah barang yang tersedia diminta, dan sebaliknya semakin naik tingkat harga semakin sedikit jumlah barang yang bersedia diminta.”
Pada hukum permintaan berlaku asumsi ceteris paribus. Artinya hukum permintaan tersebut berlaku jika situasi atau faktor-faktor selain dan tidak berubah (dianggap tetap).
Faktor-Faktor Yang Mempengaruhi Fase Permintaan (Demand)
- Harga barang itu sendiri
Harga barang akan memengaruhi jumlah barang yang diminta. Jika dan naik jumlah permintaan barang tersebut akan menurun, sedangkan jika harga turun hingga jumlah permintaan barang tetao meningkat.
- Harga barang substitusi (pengganti)
Harga barang kemudian jasa pengganti (substitusi) turut memengaruhi jumlah barang lalu jasa yang diminta. Bila harga dari barang substitusi lebih murah maka jamaah akan beralih pada barang substitusi tersebut. Akan walaupun jika harga barang substitusi naik maka orang jadi tetap menggunakan barang yang semula. Contohnya kaus merupakan pengganti kemeja. Jika dalam pasar harga kaus jauh murah dibandingkan kemeja, lalu permintaan akan kaus jauh banyak bila dibandingkan permintaan terhadap kemeja.
- Harga barang komplementer (pelengkap)
Barang pelengkap juga dapat memengaruhi permintaan barang/jasa. Misalnya sepeda engine, barang komplementernya bensin. Jika harga bensin naik, jadi kecenderungan orang untuk membeli sepeda motor akan turun, begitu juga sebaliknya.
- Kuantitas Pendapatan
Besar kecilnya pendapatan yang diperoleh seseorang turut menentukan besarnya permintaan jadi barang dan jasa. Bila pendapatan yang diperoleh banyak maka permintaan akan barang dan jasa juga makin tinggi. Sebaliknya jika pendapatannya turun, maka kemampuan utk membeli barang juga tetao turun.
Akibatnya jumlah barang akan semakin turun. Umpama pendapatan Ibu Tia untuk hasil dagang minggu mulailah Rp200. 000, 00 cuma dapat untuk membeli kopi 20 kg. Tetapi saat hasil dagang minggu kedua Rp400. 000, 00, Ibu Tia dapat membeli kopi sebanyak 40 kg.
- Selera konsumen
Selera konsumen kepada barang dan jasa meraih memengaruhi jumlah barang yang diminta. Jika selera konsumen terhadap barang tertentu naik maka permintaan terhadap barang tersebut akan meningkat jua. Misalnya, sekarang ini tidak sedikit orang yang mencari side phone yang dilengkapi servis musik dan game, sebab selera konsumen akan barang tersebut tinggi maka permintaan akan palm telephone yang dilengkapi musik dan game akan meningkat.
- Intensitas keperluan konsumen
Intensitas kebutuhan konsumen berpengaruh terhadap jumlah barang yang diminta. Kebutuhan kepada suatu barang atau service yang tidak mendesak, jadi menyebabkan permintaan masyarakat kepada barang atau jasa ini rendah.
Sebaliknya jika kepentingan terhadap barang atau service sangat mendesak maka permintaan masyarakat terhadap barang ataupun jasa tersebut menjadi naik, misalnya dengan meningkatnya curah hujan maka intensitas keperluan akan jas hujan makin meningkat. Konsumen akan bersedia membeli jas hujan maka Rp25. 000, 00 meskipun kenyataannya harga jas hujan Rp15. 000, 00.
- Perkiraan harga pada masa hadapan
Apabila konsumen memperkirakan yakni harga akan naik jadi konsumen cenderung menambah besarnya barang yang dibeli sebab ada kekhawatiran harga tetao semakin mahal. Sebaliknya bila konsumen memperkirakan bahwa dan akan turun, maka konsumen cenderung mengurangi jumlah barang yang dibeli. Misalnya nyata dugaan kenaikan petunjuk harga bahan bakar minyak mengakibatkan melimpah konsumen antri di SPBU (Stasiun Pengisian Bahan Bakar Umum) untuk mendapatkan bränsle atau solar yang berlimpah banyak.
- Jumlah masyarakat
Pertambahan penduduk akan memengaruhi kuantitas barang yang diminta. Andai jumlah penduduk dalam salahsatu wilayah bertambah banyak, jadi barang yang diminta tetao meningkat.
Macam-macam Elastisitas Harga Permintaan
Berdasarkan nilainya, elastisitas permintaan dapat dibedakan menjadi lima, yaitu permintaan inelastis sempurna, inelastis, elastis uniter, elastis, dan elastis sempurna.
- Elastisitas Silang (Cross Elasticity)
Elastisitas silang menunjukkan hubungan antara jumlah barang yang diminta terhadap perubahan harga barang lain yang mempunyai hubungan dengan barang tersebut. Hubungan tersebut dapat bersifat pengganti, dapat pula bersifat pelengkap. Terdapat tiga macam respons prubahan permintaan suatu barang (misal barang A) karena perubahan harga barang lain (barang B), yaitu: positif, negatif, dan nol.
- Elastisitas silang Peningkatan harga barang A menyebabkan peningkatan jumlah permintaan barang B. Sebagai contoh, peningkatan harga kopi meningkatkan permintaan terhadap teh. Kopi dan teh merupakan dua barang yang dapat saling menggantikan (barang substitutif).
- Elastisitas silang negatif. Peningkatan harga barang A mengakibatkan turunnya permintaan barang B. Sebagai contoh, peningkatan harga bensin mengakibatkan penurunan permintaan terhadap kendaraan bermotor. Kedua barang tersebut bersifat komplementer (pelengkap).
- Elastisitas silang Peningkatan harga barang A tidak akan mengakibatkan perubahan permintaan barang B. Dalam kaus semacam ini, kedua macam barang tidak saling berkaitan. Sebagai contoh, kenaikan harga kopi tidak akan berpengaruh terhadap permintaan kendaraan bermotor.

Dari data Tabel di atas mengenai daftar permintaan jeruk oleh Desi. Dapat di simpulkan Ketika harga jeruk Rp4.500,00/kg permintaan Desi sebesar 140 kg. Namun ketika harga jeruk Rp6.000,00/kg, permintaan turun menjadi 20 kg. Hal ini menunjukkan bahwa semakin tinggi harga suatu barang, permintaan akan turun. Kondisi tersebut menggambarkan bunyi hukum permintaan.
Hukum permintaan adalah hukum yang menjelaskan tentang adanya hubungan yang bersifat negatif antara tingkat harga dengan jumlah barang yang diminta. Apabila harga naik jumlah barang yang diminta sedikit dan apabila harga rendah jumlah barang yang diminta meningkat. Dengan demikian hukum permintaan berbunyi: Pada hukum permintaan berlaku asumsi ceteris paribus. Artinya hukum permintaan tersebut berlaku jika keadaan atau faktor-faktor selain harga tidak berubah (dianggap tetap).

Penawaran

Dari table di atas hukum penawaran dari jeruk Pak Heri. Pada tabel tersebut akan terlihat bahwa apabila harga Rp4.500,00, jumlah jeruk yang ditawarkan Pak Heri sebanyak 50 kg. Pada saat harga Rp4.750,00. Pak Heri menawarkan jeruknya sebanyak 60 kg. Hingga pada harga Rp6.000,00, jumlah jeruk yang ditawarkan sebanyak 110 kg. Apa yang dapat kalian simpulkan dari tabel di atas?
Berdasarkan tabel di atas dapat disimpulkan bahwa semakin tinggi harga, jumlah barang yang ditawarkan semakin banyak. Sebaliknya semakin rendah harga barang, jumlah barang yang ditawarkan semakin sedikit. Inilah yang disebut hukum penawaran. Hukum penawaran menunjukkan keterkaitan antara jumlah barang yang ditawarkan dengan tingkat harga. Dengan demikian bunyi hukum penawaran berbunyi:
 Hukum penawaran akan berlaku apabila faktor-faktor lain yang memengaruhi penawaran tidak berubah (ceteris paribus).
Hukum penawaran akan berlaku apabila faktor-faktor lain yang memengaruhi penawaran tidak berubah (ceteris paribus).
Penentuan Harga Keseimbangan
Dalam ilmu ekonomi, harga keseimbangan atau harga ekuilibrium adalah hargan yang terbentuk pada titik pertemuan kurva permintaan dan kurva penawaran. Terbentuknya harga dan kuantitas keseimbangan di pasar merupakan hasil kesepakatan antara pembeli dan penjual di mana kuantitas yang diminta dan yang ditawarkan sama besarnya. Jika keseimbangan ini telah tercapai, biasanya titik keseimbangan ini akan bertahan lama dan menjadi patokan pihak pembeli dan pihak penjual dalam menentukan harga. Sehingga terjadilah transaksi antara penjual dan pembeli.
Pergeseran Kurva
- Permintaan
Pergeseran kurva permintaan menunjukkan adanya perubahan permintaan yang ditimbulkan oleh faktor-faktor selain harga. Pergeseran kurva permintaan ditunjukkan dengan bergeraknya kurva ke kanan atau ke kiri. Kembali pada contoh di depan mengenai permintaan Desi terhadap jeruk. Pada contoh di depan menunjukkan bahwa berubahnya jumlah jeruk yang diminta Desi akibat dari perubahan harga jeruk itu sendiri.
Bagaimana jika faktor lainnya seperti pendapatan Desi memengaruhi jumlah jeruk yang diminta? Apabila pendapatan Desi mengalami peningkatan, maka jumlah jeruk yang diminta pun juga akan meningkat. Namun ketika pendapatan Desi mengalami penurunan maka jumlah jeruk yang diminta akan turun. Untuk lebih jelasnya perhatikan Tabel dibawah ini dan bentuk kurva berikut ini.
 Daftar Jumlah Jeruk yang Diminta Akibat Perubahan Pendapatan
Daftar Jumlah Jeruk yang Diminta Akibat Perubahan Pendapatan
Apabila dari tabel di atas diubah dalam bentuk grafik, maka akan tampak seperti di bawah ini.
Perhatikan kurva permintaan di atas. Kurva permintaan mengalami pergeseran ke kanan dari D ke D1 dan bergeser ke kiri dari D ke D2. Pergeseran ke kanan dari kurva permintaan menunjukkan pertambahan jumlah permintaan karena adanya peningkatan pendapatan. Sedangkan kurva bergeser ke kiri menunjukkan penurunan jumlah permintaan karena penurunan pendapatan. Dengan demikian dapat disimpulkan bahwa adanya perubahan pendapatan dapat mengubah jumlah permintaan akan barang serta dapat menggeser kurva permintaan.
Hukum Penawaran
Dalam hukum penawaran kita akan melihat hubungan antara harga dengan jumlah barang atau jasa yang ditawarkan. Hukum penawaran berbunyi: “Bila harga naik maka jumlah barang atau jasa yang ditawarkan akan naik, dan bila harga turun maka jumlah barang atau jasa yang ditawarkan ikut turun, dengan syarat ceteris paribus (faktor-faktor lain dianggap tidak berubah/tetap/konstan).
Dengan syarat ceteris paribus berarti hukum penawaran hanya berlaku bila faktor lain yang memengaruhi naik turunnya penawaran tidak berubah. Apabila faktor-faktor lain yang berubah (syarat ceteris paribus tidak terpenuhi) maka hukum penawaran tidak berlaku lagi. Contoh: bila harga naik, seharusnya menurut hukum penawaran, jumlah barang atau jasa yang ditawarkan akan naik, tetapi karena ada faktor lain yang berubah yakni meningkatnya biaya produksi akibatnya kenaikan harga justru diikuti oleh penurunan penawaran. Mengapa demikian? Karena kenaikan harga yang terjadi tidak sepadan dengan kenaikan biaya produksi yang begitu membengkak sehingga produsen merugi bila menambah penawarannya.
Selanjutnya, bila kita mencermati bunyi hukum penawaran di atas maka terdapat hubungan positif antara harga dengan jumlah barang atau jasa yang ditawarkan. Atau dengan istilah lain, harga berbanding lurus dengan jumlah barang/jasa yang ditawarkan, dan penurunan harga akan diikuti oleh menurunnya jumlah barang atau jasa yang ditawarkan.
Penawaran
Sama halnya pada pergeseran kurva permintaan, kurva penawaran juga dapat mengalami pergeseran karena adanya perubahan faktor-faktor yang memengaruhi penawaran selain faktor harga. Bergesernya kurva penawaran ditandai dengan bergeraknya kurva ke kanan atau ke kiri. Kurva penawaran bergeser ke kiri, artinya jumlah penawarannya mengalami kenaikan.
Namun, ketika kurva penawaran barang bergeser ke kiri, berarti terjadi penurunan penawaran barang. Misalnya diperkirakan harga jeruk bulan depan akan naik karena harga pupuk naik. Kenaikan harga jeruk menyebabkan penurunan penawaran jeruk. Sehingga ketika diperkirakan harga di masa depan naik, maka penjual akan mengurangi jumlah barang yang dijualnya. Tabel berikut ini yang akan menunjukkan jumlah jeruk yang ditawarkan Pak Heri sebelum dan sesudah kenaikan harga.
Daftar Jumlah Jeruk yang Ditawarkan Akibat Perubahan Kenaikan Harga
Tabel di atas jika dibuat grafik akan tampak seperti berikut ini.
 Perhatikan kurva penawaran di atas. Kurva penawaran S bergeser ke kiri menjadi S1. Hal ini menunjukkan bahwa jumlah penawaran akan jeruk mengalami penurunan. Penurunan kurva penawaran jeruk tersebut sebagai akibat dari meningkatnya harga pupuk. Jadi dapat disimpulkan bahwa adanya perubahan dari salah satu atau lebih faktor-faktor yang dulu dianggap tetap, akan mengubah jumlah penawaran sekaligus menggeser kurva penawaran.
Perhatikan kurva penawaran di atas. Kurva penawaran S bergeser ke kiri menjadi S1. Hal ini menunjukkan bahwa jumlah penawaran akan jeruk mengalami penurunan. Penurunan kurva penawaran jeruk tersebut sebagai akibat dari meningkatnya harga pupuk. Jadi dapat disimpulkan bahwa adanya perubahan dari salah satu atau lebih faktor-faktor yang dulu dianggap tetap, akan mengubah jumlah penawaran sekaligus menggeser kurva penawaran.
Fungsi Penawaran
Berdasarkan bunyi hukum penawaran, terlihat adanya hubungan antara harga dengan jumlah barang atau jasa yang ditawarkan. Hubungan tersebut dapat dinyatakan dalam bentuk fungsi yang disebut dengan fungsi penawaran. Jadi, yang dimaksud dengan fungsi penawaran adalah fungsi yang menunjukkan hubungan antara tingkat harga (P) dengan jumlah barang atau jasa yang ditawarkan (Q), yang dirumuskan sebagai berikut:

Qs P (jumlah barang atau jasa yang ditawarkan) merupakan fungsi dari P (harga). Artinya, banyak sedikitnya Qs bergantung pada besar kecilnya P (harga). Fungsi tersebut di atas bila ditulis dalam bentuk persamaan linear sederhana akan tampak sebagai berikut:
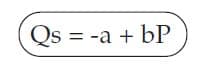 Keterangan:
Keterangan:
Qs= jumlah barang atas jasa yang ditawarkan
P = harga
a = konstanta
b = koefisien (b bertanda positif karena harga dan jumlah barang atau jasa yang ditawarkan memiliki hubungan positif).
Contoh fungsi penawaran adalah Q = –3 + 20P.
Fungsi ini bisa ditulis menjadi Q = 20P –3 atau bisa pula ditulis menjadi -20P = –Q-3
Berikutnya akan diuraikan cara menggambar kurva penawaran berdasarkan fungsi penawaran yang sudah diketahui. Cara menggambarnya sama dengan cara menggambar kurva permintaan. Misalnya, kita diminta menggambarkan fungsi penawaran Qs = – 10, 10P, maka langkahnya adalah:
Diketahui Qs = –10 + 10P

Kadang-kadang kita harus mencari terlebih dahulu fungsi penawaran dari suatu kumpulan data penawaran. Berdasarkan data penawaran itulah kita mencari bagaimana fungsi penawarannya. Untuk mencarinya, kita menggunakan rumus persamaan garis lurus melalui dua titik yang juga digunakan dalam mencari fungsi permintaan, sebagai berikut.

Carilah:
- Fungsi penawarannya.
- Berdasarkan fungsi penawaran tersebut, tentukan berapa Q (jumlah yang ditawarkan) bila P = Rp1.000,-?
Jawab :
Untuk mencari fungsi penawaran, pilihlah dua pasang data dari tabel di atas, misalnya kita pilih P = 100, Q = 10 dan P = 250, Q = 20.
Dengan demikian P1 = 150 dan Q1 = 10
P2 = 250 dan Q2 = 20

Sekian penjelasan artikel diatas tentang Hukum Permintaan semoga dapat ber,anfaatpat bermanfaat bagi pembaca setia DosenPendidikan.Co.Id