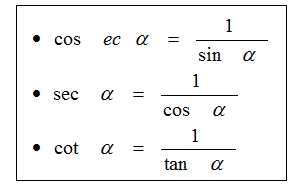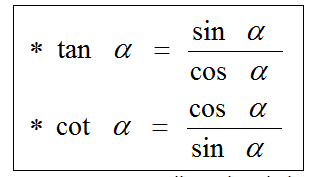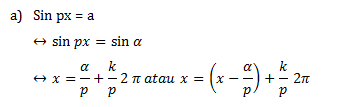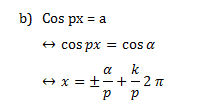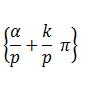Identitas Trigonometri – Sudut Istimewa, Sifat, Rumus Dan Contoh – Trigonometri (dari bahasa Yunani trigonon = “tiga sudut” dan metron = “mengukur”) adalah sebuah cabang matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga. Bidang ini muncul di masa Hellenistik pada abad ke-3 SM dari penggunaan geometri untuk mempelajari astronomi.
Identitas Trigonometri
Jika salah satu satu sudut 90 derajat dan sudut lainnya diketahui, dengan demikian sudut ketiga dapat ditemukan, karena tiga sudut segitiga bila dijumlahkan menjadi 180 derajat. Karena itu dua sudut (yang kurang dari 90 derajat) bila dijumlahkan menjadi 90 derajat: ini sudut komplementer.
Kegunaan
Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan “penyebaran” dan “quadrance”, bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales. Informasi lebih lanjut bisa dilihat di situs webnya.
Rumus – Rumus yang perlu dipahami
- Rumus Dasar yang merupakan Kebalikan
- Rumus Dasar yang merupakan hubungan perbandingan
- Rumus Dasar yang diturunkan dari teorema phytagoras
- Contoh 1
Buktikan identitas berikut:
- Sin α . Cos α . Tan α = (1 – Cos α) (1 + Cos α)
Jawab:
- Sin β . Tan β + Cos β = Sec β
Jawab:
Baca Juga: Rumus Volume Tabung
Persamaan Trigonometri
Persamaan trigonometri dapat diselesaikan dengan menggunakan daftar atau menggunakan rumus-rumus perbandingan sudut-sudut berelasi.
Periodisitas Trigonometri
Teorema :
Fungsi f(x) = sin x dan g(x) = cos x adalah fungsi periodik yang berperiode dasar 360. Sedangkan fungsi h(x) = tan (x) dan g(x) = cotg (x) adalah fungsi periodik yang berperiode dasar 180. Dengan demikian dapat diketahui :
- Persamaan Trigonometri Sederhana
Baca Juga : “Listrik Dinamis” Pengertian & ( Rumus – Contoh )
- Contoh 2
Tentukan himpunan Penyelesaian dari Persamaan Sin x =
Jawaban :
- Persamaan Trigonometri dalam bentuk a cos x + b sin x = c
Cara penyelesaian persamaan tersebut di atas sebagai berikut:
Baca Juga : “Listrik Statis” Pengertian & ( Konsep Dasar – Contoh – Rumus )
- Contoh 3
Tentukan himpunan penyelesaian dari persamaan:
Cos y – Sin y = 1, jika 0o ≤ y ≤ 360o
Jawab:
Cos y – Sin y = 1 ↔ a = 1; b = – 1 ; c = 1
- Persamaan Trigonometri yang berbentuk Sin px = a, cos px = a, dan tan px = a, dengan a dan p adalah konstanta
Penyelesaian persamaan trigonometri yang berbentuk Sin px = a, cos px = a dan
tan px = a dapat dilakukan dengan cara mengubah persamaan-persamaan trigonometri tersebut menjadi persamaan trigonometri dasar.
Teorema:
Himpunan Penyelesaian umum adalah :
Himpunan Penyelesaian umum adalah :
Himpunan Penyelesaian umum adalah
Baca Juga : Rumus Cermin Cembung
- Persamaan Trigonometri yang memuat jumlah atau selisih sinus atau kosinus
Untuk menentukan himpunan penyelesaian persamaan trigonometri yang memuat jumlah atau selisih sinus kosinus, diperlukan rumus penjumlahan dan pengurangan sinus dan kosinus sebagai berikut :
Contoh :
Tentukan himpunan penyelesaian dari persamaan trigonometri :
Jawab:
Jadi, Himpunan Penyelesaian persamaan
Baca Juga : Asam Asetat – Pengertian, Rumus, Reaksi, Bahaya, Sifat Dan Penggunaannya
- Persamaan Trigonometri yang dapat diubah menjadi persamaan kuadrat dalam sinus, kosinus atau tangens
Pada dasarnya sebuah persamaan trigonometri yang dapat diubah menjadi persamaan kuadrat dapat dicari penyelesaianya menggunakan faktorisasi, melengkapkan bentuk persamaan kuadrat sempurna atau dengan rumus abc dengan memperhatikan sifat-sifat dari trigonometri.
Contoh :
Bentuk a cos x + b sin x
Bentuk a cos x + b sin x bisa diubah menjadi
a cos x + b sin x = k cos (x – α)
Nilai k dan α tidak ada di ruas kiri, sehingga bisa dicari dengan cara sebagai berikut
- a cos x + b sin x = k cos (x – α)
- a cos x + b sin x = k [cos x cos α + sin x sin α]
- a cos x + b sin x = k cos x cos α + k sin x sin α
- a cos x + b sin x = k cos α cos x + k sin α sin x
Maka :
Jika k sin α dan k cos α kita bagikan maka diperoleh
Kesimpulan
a cos x + b sin x = k cos (x – α)
dengan
Dan
Baca Juga : Hukum Kepler 1 2 3 – Konsep, Rumus, Sejarah, Contoh Soal
- Contoh soal
- Ubahlah bentuk cos x + √3sinx menjadi bentuk k cos (x – α)!
Penyelesaian :
Jadi, cosx + √3sinx dapat di ubah menjadi 2cos(x – 60°)
- Ubahlah bentuk -√3 cos x + sin x menjadi bentuk k cos (x – α)!
Penyelesaian :
Jadi, -√3 cosx + sin x dapat di ubah menjadi 2 cos (x – 150°)
Demikian penjelasan diatas tentang Identitas Trigonometri – Sudut Istimewa, Sifat, Rumus Dan Contoh semoga bermanfaat bagi semua pembaca DosenPendidikan.Com