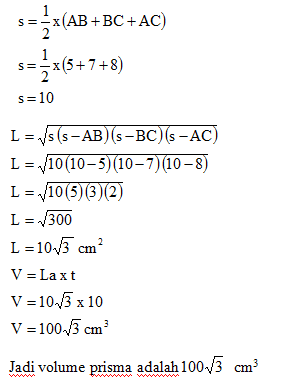Pengertian Prisma
Prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Dengan kata lain prisma adalah bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran.
Prisma segi-n memiliki n + 2 sisi, 2n titik sudut, dan 3n rusuk. Prisma dengan alas dan tutup berbentuk persegi disebut balok sedangkan prisma dengan alas dan tutup berbentuk lingkaran disebut tabung.
Pengertian lain Prisma adalah bangun ruang yang dibatasi oleh dua buah bidang segi banyak (segi-n) yang sejajar dan kongruen serta bidang-bidang tegak yang menghubungkan bidang segi banyak tersebut.
Baca Juga Artikel yang Mungkin Berkaitan : 1 Kg Berapa Liter
Unsur-Unsur Prisma
Macam-macam unsur prisma berdasarkan bentuk alas dan tutup nya adalah sebagai berikut:
-
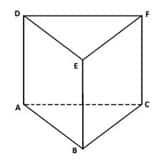
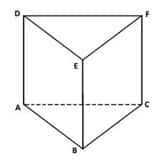
Prisma Segitiga ABC.DEF
Prisma segitiga ABC.DEF seperti gambar 1.1 di atas memiliki unsur-unsur sebagai berikut:
- Mempunyai 6 titik sudut, yaitu : Titik A, B, C, D, E, dan F
- Mempunyai 9 rusuk , yaitu : Rusuk alas AB, BC, dan AC; Rusuk atas DE, EF, dan DF Rusuk tegak AD. BE, dan CF
- Mempunyai 5 bidang sisi, yaitu : Sisi alas ABC ; sisi atas DEF dan Sisi tegak ABED, BCFE dan ACFD
-
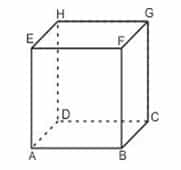
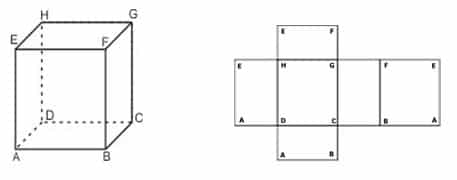
Prisma Segiempat ABCD.EFGH
Prisma segiempat ABCD.EFGH seperti gambar 1.2 di atas memiliki unsur-unsur sebagai berikut:
- Mempunyai 8 titik sudut, yaitu : Titik A, B, C, D, E, F, G dan H
- Mempunyai 12 rusuk , yaitu : Rusuk alas AB, BC, CD dan DA; Rusuk atas EF, FH, GH, dan EG Rusuk tegak EA. FB, HC, dan GD
- Mempunyai 8 bidang sisi, yaitu : sisi alas ABCD ; sisi atas EFGH dan sisi tegak ABFE, BCGF, CDHG dan ADHE
- Mempunyai 12 diagonal bidang, yaitu : AC, BD, EG, HF, BG, CF, CH, DG, AH, DE, AF, dan BE.
- Mempunyai 4 diagonal ruang, yaitu: AG, CE, BH dan DF
Baca Juga Artikel yang Mungkin Berkaitan : Jaring Jaring Balok
-
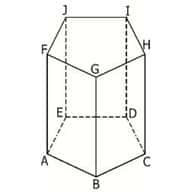
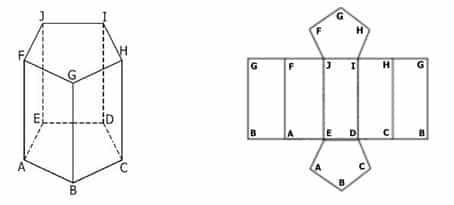
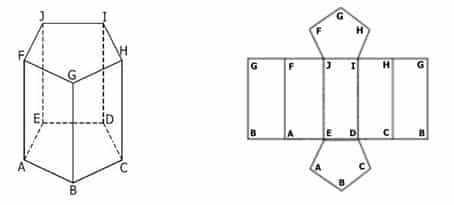
Prisma Segilima ABCDE.FGHIJ
Prisma segilima ABCDE.FGHJI seperti gambar 1.3 di atas memiliki unsur-unsur sebagai berikut:
- Mempunyai 10 titik sudut, yaitu : Titik A, B, C, D, E, F, G, H, I, dan J
- Mempunyai 15 rusuk , yaitu : Rusuk alas AB, BC, CD, DE dan EA Rusuk atas FG, GH, HI, IJ dan JF Rusuk tegak FA. GH, HI, IJ dan JE
- Mempunyai 7 bidang sisi, yaitu : Sisi alas ABCDE ; sisi atas FGHIJ Sisi tegak ABGF, BCHG, CDIH, DEJI, dan AEJF
-
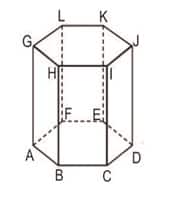
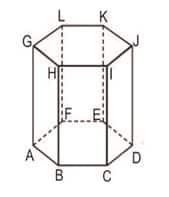
Prisma Segienam ABCDEF.GHIJKL
Prisma segienam ABCDEF.GHIJKL seperti gambar 1.4 di atas memiliki unsur-unsur sebagai berikut:
- Mempunyai 12 titik sudut, yaitu : Titik A, B, C, D, E, F, G, H, I, J, K, dan L
- Mempunyai 18 rusuk , yaitu : Rusuk alas AB, BC, CD, DE, EF dan FA ;
Rusuk atas GH, HI, IJ, JK, KL dan LG
Rusuk tegak GA. HB, IC, JD, KE dan LF
- Mempunyai 8 bidang sisi, yaitu : Sisi alas ABCDEF ; sisi atas GHIJKL dan Sisi tegak ABHG, BCIH, CDJI, DEKJ, EFLK dan FAGL
Macam-macam jaring prisma berdasarkan bentuk alas dan tutup adalah sebagai berikut:
Baca Juga Artikel yang Mungkin Berkaitan : Jaring-Jaring Kubus
-
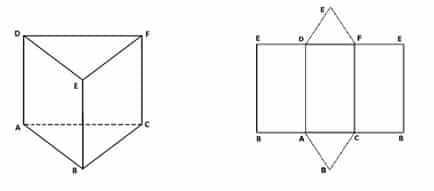
Prisma Segitiga ABC.DEF
Gambar 1 Gambar 2
Pada gambar 1 adalah bangun ruang prisma segitiga, jika kita ingin mencari jaring-jaringnya, maka kita dapat membuka bangun ruang prisma tersebut. Sehingga akan diperoleh jaring-jaring seperti pada gambar 2.
-
Prisma Segiempat ABCD.EFGH
Gambar 1 Gambar 2
Pada gambar 1 adalah bangun ruang prisma segiempat, jika kita ingin mencari jaring-jaringnya, maka kita dapat membuka bangun ruang prisma tersebut. Sehingga akan diperoleh jaring-jaring seperti pada gambar 2.
-
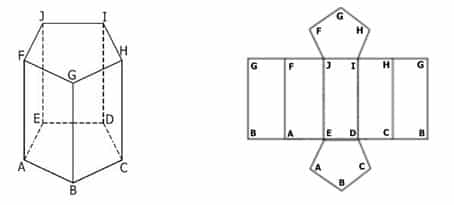
Prisma Segilima ABCDE.FGHIJ
Gambar 1 Gambar 2
Pada gambar 1 adalah bangun ruang prisma segilima, jika kita ingin mencari jaring-jaringnya, maka kita dapat membuka bangun ruang prisma tersebut. Sehingga akan diperoleh jaring-jaring seperti pada gambar 2.
-
Prisma Segienam ABCDEF.GHIJKL
Gambar 1 Gambar 2
Pada gambar 1 adalah bangun ruang prisma segienam, jika kita ingin mencari jaring-jaringnya, maka kita dapat membuka bangun ruang prisma tersebut. Sehingga akan diperoleh jaring-jaring seperti pada gambar 2.
Rumus Prisma
Berikut ini terdapat beberapa rumus-rumus prisma, terdiri atas:
1. Rumus Volume Prisma
Volume Prisma = Luas alas x tinggi
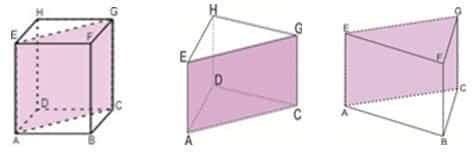
Untuk menentukan rumus umum volume sebuah prisma, marilah kita tinjau rumus volume prisma segitiga. Rumus volume prisma segitiga dapat diturunkan dari rumus volume balok. Perhatikanlah gambar berikut ini:
Jika balok ABCD.EFGH pada gambar (a) dibagi dua melalui bidang diagonal ACGE maka akan diperoleh dua buah prisma segitiga, yaitu prisma ACD.EGH dan prisma ABC.EFG. Karena bidang diagonal balok membagi balok menjadi dua bagian sama besar, maka volume balok sama dengan dua kali volume prisma segitiga. Maka volume prisma segitiga dapat dirumuskan:
Baca Juga Artikel yang Mungkin Berkaitan : Transformasi Geometri
Apakah untuk menentukan rumus volume prisma yang lain dapat menggunakan rumus volume prisma segitiga? Perhatikan gambar di bawah ini!
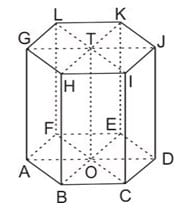
Jika prisma segienam beraturan kita iris pada bidang diagonal ADJG, bidang diagonal BEKH, dan bidang diagonal CFLI, maka kita akan mendapatkan enam buah prisma segitiga beraturan. Maka volume prisma segienam dapat dinyatakan dalam bentuk berikut:
Volume prisma segienam ABCDEF.GHIJKL
= 6 × volume prisma segitiga BCO.HIT
= 6 × luas BCO×TO
= luas segienam ABCDEF×TO
= luas alas × tinggi prisma
Maka untuk setiap prisma berlaku rumus:
Volume prisma = luas alas × tinggi prisma
Jika kita ingin menentukan volume prisma, terlebih dulu kita mencari luas alas prisma. Luas alas dicari sesuai dengan bentuk alas. Kemudian kita mencari tinggi prisma. Setelah luas alas dan tinggi prisma diketahui, kita dapat mencari volume prisma dengan mengalikan luas alas prisma dengan tinggi prisma. Rumus volume prisma berdasarkan bentuk alas dan tutupnya:
- Rumus volume prisma untuk segitiga
Volume prisma segitiga = (½ × alas segitiga × tinggi segitiga) × tinggi prisma
- Rumus volume prisma untuk segiempat sama sisi
Volume prisma segi empat sama sisi = (sisi × sisi) × tinggi prisma
- Rumus volume prisma segi empat
Volume prisma segi empat = (panjang × lebar) × tinggi prisma
- Rumus volume prisma segi lima
Volume prisma segi lima= 5 x (1/2 × alas segitiga × tinggi segitiga) × tinggi prisma.
- Rumus volume prisma segi enam
Volume prisma segi enam = 6 x (1/2) × alas segitiga × tinggi segitiga) × tinggi prisma.
2. Rumus Luas Permukaan Prisma
Luas permukaan prisma = (2 × luas alas) + (keliling alas × tinggi prisma)
Misalkan kita memiliki prisma segilima ABCDE.FGHIJ seperti terlihat pada gambar 2.17 dan bentuk jaring-jaringnya pada gambar 2.18. Maka luas permukaan prisma adalah sebagai berikut:
Gambar 1 Gambar 2
Luas permukaan prisma segilima ABCDE.FGHIJ = luas bidang EABCD + luas bidang IHGFJ + luas bidang EDIJ + luas bidang DCHI + luas bidangCBGH + luas bidangBAFG + luas bidangAEJF.
Karena bidang alas dan bidang tutup prisma kongruen, maka luas EABCD = luas IHGFJ, sehingga dapat dinyatakan dalam bentuk berikut:
Luas permukaan prisma= luas bidang EABCD + luas bidang EABCD + a × t + a × t + a × t + a × t + a × t
= 2 × luasEABCD + (a + a + a + a + a) × t
= (2 × luas alas) + (keliling alas × tinggi prisma)
Maka untuk setiap prisma berlaku rumus:
Luas permukaan prisma = (2 × luas alas) + (keliling alas × tinggi prisma)
Selain cara di atas dapat juga luas permukaan di cari menggunakan tabel sebagai berikut:
| Prisma segi | Luas alas atau tutup | Jumlah luas sisi tegak |
| tiga | x a x t | 3 x ( p x l ) |
| empat | S2 | 4 x ( p x l ) |
| lima | x a x t | 5 x ( p x l ) |
| enam | x a x t | 6 x ( p x l ) |
| .. | ..
.
|
..
.
|
| n | Luas alas segi-n | n x ( p x l ) |
karena bentuk alas dan tutup prisma tersebut sama, jadi rumus luas permukaan prisma = (2 x luas alas segi n + jumlah luas sisi tegak n).
Contoh Soal Prisma
a. Contoh Soal SMP dan Pembahasannya
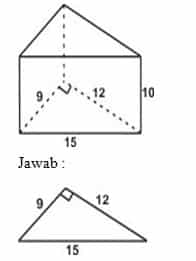
1. Alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi masing-masing 9 cm, 12 cm, dan 15 cm. Jika tinggi prisma 10 cm, hitunglah luas permukaan prisma itu!
Jawab:
Luas permukaan prisma
= ( 2 x luas alas ) + (keliling alas x tinggi)
= [2 x ( x 9 x 12 )] +[(9 + 12 + 15) x 10]
= (2 x 54) + (36 x 10 )
= 108 + 360
= 468
Jadi, luas permukaan prisma adalah 468 cm².
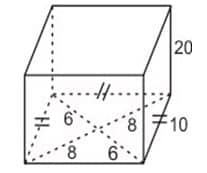
2. Alas sebuah prisma berbentuk belah ketupat dengan panjang sisi 10 cm dan panjang diagonalnnya masing-masing 12 cm dan 16 cm. Jika tinggi prisma 20 cm, hitunglah luas permukaan prisma tersebut !
Jawab:
Luas permukaan prisma
= (2 x luas alas) + (keliling alas x tinggi)
= + [(4 x 10) x 20]
= (2 x 96) + (40 x 20)
= 192 + 800
= 992
Jadi, luas permukaan prisma adalah 992 cm2.
Baca Juga Artikel yang Mungkin Berkaitan : Pertidaksamaan Nilai Mutlak
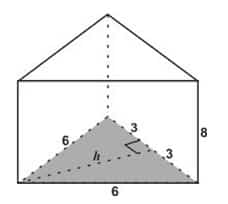
3. Alas sebuah prisma berbentuk segitiga sama sisi dengan panjang sisi-sisinya 6 cm. Hitunglah luas permukaan prisma tersebut, jika tinggi prisma 8 cm!
Jawab:
Terlebih dahulu kita hitung tinggi segitiga alas, yaitu:
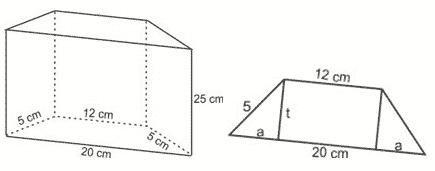
6. Alas sebuah prisma berbentuk trapesium sama kaki dengan panjang sisi-sisi sejajarnya adalah 12 cm dan 20 cm, serta sisi miringnya 5 cm. Jika tinggi prisma tersebut 25 cm, hitunglah volume prisma!
Jawab:
b. Contoh Soal SMA dan Pembahasannya
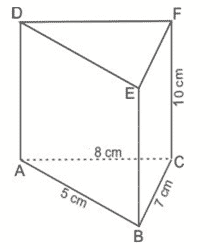
1. Diketahui prisma segitiga tegak ABC.DEF. Volume prisma tersebut adalah … cm3
Alas prisma berbentuk segitiga. Luas segitiga adalah…
Jawab:
Baca Juga Artikel yang Mungkin Berkaitan : Sin Cos Tan
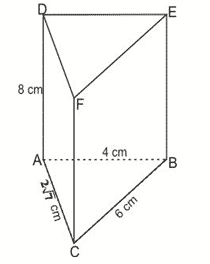
2. Diketahui prisma tegak segitiga tegak ABC.DEF. Panjang AB = 4 cm, BC = 6 cm, AC = 2√7 cm, dan CF = 8 cm. Volume prisma tersebut adalah ….
Jawab:
Demikianlah pembahasan mengenai Rumus Prisma – Pengertian, Unsur Beserta Contoh Soal SMP, SM semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua, terima kasih banyak atas kunjungannya. 🙂 🙂 🙂