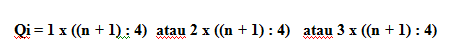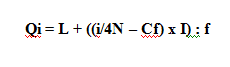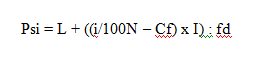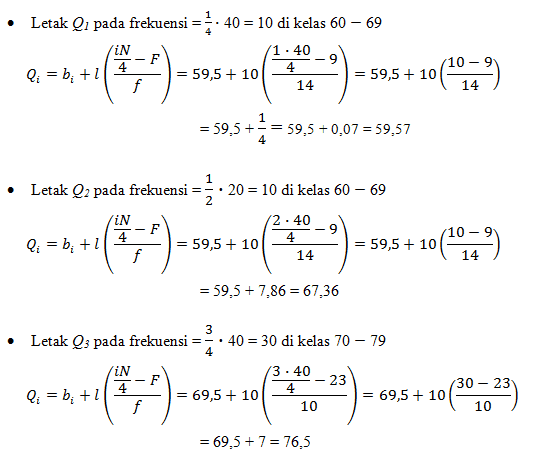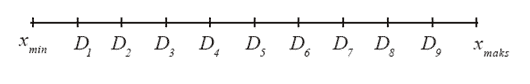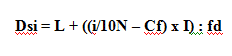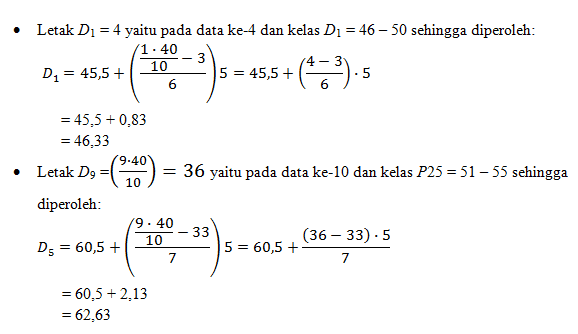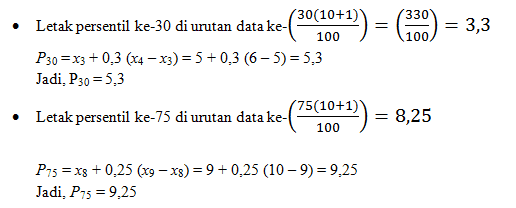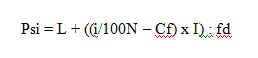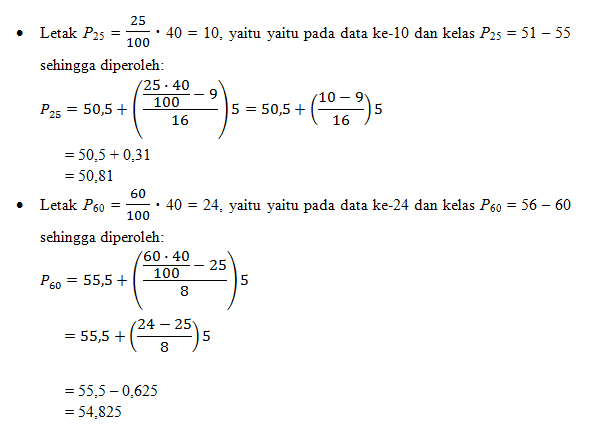Rumus Kuartil, Desil dan Persentil – Contoh Soal dan Jawaban – Untuk pembahasan kali ini kami akan mengulas mengenai Kuartil, Desil dan Persentil yang dimana dalam hal ini meliputi rumus, pengertian, contoh soal dan jawaban, nah untuk lebih memahami dan mengerti simak ulasan dibawah ini.
Pengertian Kuartil
Kuartil adalah ukuran letak yang membagi data yang telah diukur atau data yang berkelompok menjadi empat bagian yang sama besar.
Istilah kuartil dalam kehidupan kita sehari-hari lebih dikenal dengan istilah kuartal.
Dalam dunia statistik, yang dimaksud dengan kuartil ialah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi ke dalam empat bagian yang sama besar, yaitu masing masing sebesar ¼ N.
Jadi disini akan kita jumpai tiga buah kuartil, yaitu kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3).
Baca Juga Artikel yang Mungkin Terkait : “Kecerdasan Logika Matematika ( Logic Smart )” Pengertian & ( Ciri – Komponen – Cara Melatih )
Ketiga kuartil inilah yang membagi seluruh distribusi frekuensi dari data yang kita selidiki menjadi empat bagian yang sama besar, masing-masing sebesar ¼ N, seperti terlihat dibawah ini.
Jalan pikiran serta metode yang digunakan adalah sebagaimana yang telah kita lakukan pada saat kita menghitung median. Hanya saja,
kalau median membagi seluruh distribusi data menjadi dua bagian yang sama besar, maka kuartil membagiseluruh distribusi data menjadi empat bagian yang sama besar.
Cara menentukan kuartil dibagi menjadi 2 tipe, antara lain sebagai berikut:
1. Kuartil Data Tunggal
Rumus Kuartil Data Tunggal
Contoh Soal Kuartil Data Tunggal
Tentukan Q1, Q2 dan Q3 dari data:3, 4, 7, 8, 7, 4, 8, 4, 9, 10, 8, 3, 7, 12
Jawaban:
Data yang telah di urutkan: 3, 3, 4, 4, 4, 7, 7, 7, 8, 8, 8, 9, 10, 12
Letak Q1 adalah 1 (14+1)/4 = 15/4 = 3 ¾
Q1 =X3 + ¾ (X4 – X3)
= 4 + ¾ (4-4) = 4
Letak Q2 adalah 2 (14+1)/4 = 15/2 = 7 ½
Q2 =X7 + ½ (X7 – X6)
= 7 + ½ (7-7) = 7
Letak Q3 adalah 3 (14+1)/4 = 45/4 = 11 ¼
Q3 =X11 + ¼ (X12 – X11) = 8 + ¼ (9-8)
= 8 + ¼ (9-8)
= 8 ¼ atau 8,25
Baca Juga Artikel yang Mungkin Terkait : Cara Menghitung Persen : Pengertian Dan ( Rumus – Contoh )
2. Kuartil Data Kelompok
Rumus Kuartil Data Kelompok
Keterangan:
Q = Kuartil
L = Titik bawah
N = Banyak data
i = Kuartil 1, 2, 3
Cf = Frekuensi komulatif – sebelum kelas
f = Frekuensi kelas kuartil
I = Panjang kelas
Contoh Soal Kuartil Data Kelompok
Tentukan kuartil 1 dan 3 dari data table berikut:
| Interval | f |
| 87-108 | 2 |
| 109-130 | 6 |
| 131-152 | 10 |
| 153-174 | 4 |
| 175-196 | 3 |
| 25 |
Jawaban:
Q1 (kuartil 1)
N = 25
1/4N = ¼ x 25 = 6.25
L = 109 – 0.5 = 108.5
Cf = 2
F = 6
I = 22
Q1 = L + ((1/4N – Cf) x I) : f
= 108.5 + ((6.25 – 2) x 22) : 6
= 108.5 + (4.25 x 22) : 6
= 108.5 + 93.5 : 6
= 108.5 + 15.58
= 124.08
Baca Juga Artikel yang Mungkin Terkait : Pengertian Variabel Beserta Macam-Macamnya Menurut Para Ahli
Jawaban:
Q3 (kuartil 3)
N = 25
3/4N = 3/4 x 25 = 18.75
L = 153 – 0.5 = 152.5
Cf = 2 + 6 + 10 = 18
F = 4
I = 22
Q3 = L + ((3/4N – Cf) x I) : f
= 152.5 + ((18.75 – 18) x 22) : 4
= 152.5 + (0.75 x 22) : 4
= 152.5 + 16.5 : 4
= 152.5 + 4.125
= 156.625
Pengertian Desil
Desil adalah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi dari data yang kita selidiki ke dalam 10 bagian yang sama besar, yang masing-masing sebesar 1/10 N.
Jadi disini kita jumpai sebanyak 9 buah titik desil, dimana kesembilan buah titik desil itu membagi seluruh distribusi frekuensi ke dalam 10 bagian yang sama besar.
Kegunaan desil adalah untuk menggolongkan-golongkan suatu distribusi data ke dalam sepuluh bagian yang sama besar, kemudian menempatkan subjek-subjek penelitian ke dalam sepuluh golongan tersebut.
Cara menentukan desil dibagi menjadi 2 tipe, antara lain sebagai berikut:
Baca Juga Artikel yang Mungkin Terkait : “Algoritma” Pengertian & ( Tujuan – Fungsi – Manfaat – Sifat – Ciri )
1. Desil Data Tunggal
Rumus Desil Data Tunggal
Contoh Soal Desil Data Tunggal
Diketahui data: 9,10, 11, 6, 8, 7, 7, 8, 9, 10, 11. Tentukanlah:
- Desil ke -2
- Desil ke- 4
Jawaban:
Data di urutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10
Letak desil ke- 2 diurutan data ke- 2(10+1)/10 = 22/10 = 2,2
D2 terletak pada urutan ke- 2,2 sehingga
D2 = X2 + 0,2 (X3-X2)
D2 = 5 + 0,2 (5-5)
= 5 + 0
= 5
Letak desil ke- 2 diurutan data ke- 4(10+1)/10 = 44/10 = 4,4
D4 terletak pada urutan ke- 4,4 sehingga
D4 = X4 + 0,4 (X5-X4)
D4 = 6 + 0,4 (7-6)
= 6 + 0,4
= 6,4
2. Desil Data Kelompok
Rumus Desil Data Kelompok
Keterangan:
D = Desil
L = Titik bawah
N = Banyak data
I = Desil 1, 2, 3 … 10
Cf = Frekuensi komulatif – sebelum kelas
Fd = Frekuensi kelas desil
I = Panjang kelas
Contoh Soal Desil Data Kelompok
Tentukan Desil 7 dari data table berikut:
| Interval | f |
| 87-108 | 2 |
| 109-130 | 6 |
| 131-152 | 10 |
| 153-174 | 4 |
| 175-196 | 3 |
| 25 |
Jawaban:
Ds 7 (desil 7)
N = 25
7/10N = 7/10 x 25 = 17.5
L = 131 – 0.5 = 130.5
Cf = 2 + 6 = 8
Fd = 10
I = 22
Ds 7 = L + ((7/10N – Cf) x I) : fd
= 130.5 + ((17.5 – 8) x 22) : 10
= 130.5 + (9.5 x 22) : 10
= 130.5 + 209 : 10
= 130.5 + 20.9
= 151.4
Pengertian Persentil (Ps)
Presentil adalah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi dari data yang kita selidiki ke dalam 100 bagian yang sama besar, karena itu presentil sering disebut ukuran perseratusan.
Persentil yang biasa dilambangkan P, adalah titik atau nilai yang membagi suatu distribusi data menjadi seratus bagian yang sama besar. Karena itu persentil sering disebut ukuran perseratusan.
Titik yang membagi distribusi data ke dalam seratus bagian yang sama besar itu ialah titik-titik: P1, P2, P3, P4, P5, P6, … dan seterusnya, sampai dengan P99.
Jadi disini kita dapati sebanyak 99 titik persentil yang membagi seluruh distribusi data ke dalam seratus bagian yang sama besar, masing-masing sebesar 1/ 100N atau 1%.
Cara menentukan presentil dibagi menjadi 2 tipe, antara lain sebagai berikut:
1. Persentil Data Tunggal
Rumus Persentil Data Tunggal
Contoh Soal Persentil Data Tunggal
Tentukan letak P20 serta nilainya dari data berikut ini: 35, 40, 70, 80, 91, 50, 61, 25, 95.
Jawaban:
Data diurutkan dari data terkecil hingga terbesar ; 15, 35, 40, 50, 61, 70, 80, 91, Letak persentil 20 (P20) adalah + _____ =2. Jadi persentil ke 20 terletak pada data ke-2, yaitu 35.
2. Persentil Data Kelompok
Rumus Persentil Data Kelompok
Keterangan:
D = Presentil
L = Titik bawah
N = Banyak data
I = Persentil 1, 2, 3 … 100
Cf = Frekuensi komulatif – sebelum kelas
Fd = Frekuensi kelas presentil
I = Panjang kelas
Contoh Soal Persentil Data Kelompok
Tentukan presentil 94 dari data table berikut:
| Interval | f |
| 87-108 | 2 |
| 109-130 | 6 |
| 131-152 | 10 |
| 153-174 | 4 |
| 175-196 | 3 |
| 25 |
Jawaban:
Ps 94
N = 25
94/100N = 94/100 x 25 = 23.5
L = 175 – 0.5 = 174.5
Cf = 2 + 6 + 8 + 10 + 4 = 22
Fps = 3
I = 22
Ps94 = L + ((94/100N – Cf) x I) : fd
= 174.5 + ((23.5 – 22) x 22) : 3
= 174.5 + (1.5 x 22) : 3
= 174.5 + 33 : 3
= 174.5 + 11
= 185.5
Kegunaan persentil dalam dunia pendidikan adalah:
- Persentil dapat digunakan untuk menentukan kedudukan seorang anak didik, yaitu: pada persentil keberapakah anak didik itu memperoleh kedudukan ditengah-tengah kelompoknya.
- Persentil juga dapat digunakan sebagai alat untuk menetapkan nilai batas lulus pada tes atau seleksi.
Contoh Soal dan Jawaban Kuartil, Desil, Persentil
A. Kuartil
- Data Tunggal
a. Tentukan Q1, Q2, dan Q3 dari data : 3, 4, 7, 8, 7, 4, 8, 4, 9, 10, 8, 3, 7, 12.
Jawab:
Data yang telah diurutkan: 3, 3, 4, 4, 4, 7, 7, 7, 8, 8, 8, 9, 10, 12.
Letak dari Qi dirumuskan sebagai berikut:
Jadi, kuartil dari data tersebut yaitu:
Q1 = 4
Q2 = 7
Q3 = 8,25
b. Dalam suatu tes terhadap 50 siswa didapat tabel frekuensi tunggal sebagai berikut.
| Nilai | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Frekuensi | 3 | 5 | 6 | 8 | 12 | 6 | 7 | 3 |
Berdasarkan data di atas, tentukan kuartil ke-2.
Jawab:
Banyaknya data 50.
Jadi, kuartil ke-2 adalah 6.
- Data Kelompok
Tentukan Q1 (kuartil bawah), Q2 (median), dan Q3 (kuartil atas) dari data tes Matematika terhadap 40 siswa kelas XI IPA berikut ini.
| Nilai | Frekuensi |
| 40 – 4950 – 59
60 – 69 70 – 79 80 – 89 90 – 99 |
45
14 10 4 3 |
Jawab:
| Nilai | Frekuensi | F kumulatif |
| 40 – 4950 – 59
60 – 69 70 – 79 80 – 89 90 – 99 |
45
14 10 4 3 |
4 239 33 37 40 |
Untuk menentukan letak kuartil data kelompok, nilai kuartil dirumuskan sebagai berikut.
Keterangan:
Qi = kuartil ke-i (1, 2, atau 3)
bi = tepi bawah kelas kuartil ke-i
N = banyaknya data
F = frekuensi kumulatif kelas sebelum kelas kuartil
l = lebar kelas
f = frekuensi kelas kuartil
Jadi, kuartil dari data tersebut yaitu:
Q1 = 59,57
Q2 = 67,36
Q3 = 76,5
B. Desil
- Data Tunggal
Diketahui data: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5. Tentukan:
- desil ke-2
- desil ke-4
Jawab:
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
Letak dari Di (desil ke-i) diringkas
Keterangan:
Di = desil ke-i
I = 1, 2, 3, . . ., 9
n = banyaknya data
 Jadi, desil ke-2 dari data tersebut yaitu 5,0 dan desil ke-4 dari data tersebut yaitu 6,4.
Jadi, desil ke-2 dari data tersebut yaitu 5,0 dan desil ke-4 dari data tersebut yaitu 6,4.
- Data Kelompok
Diketahui data pada tabel data kelompok di bawah.
| x | f |
| 41 – 4546 – 50
51 – 55 56 – 60 61 – 65 |
36
16 8 7 |
Dari data tersebut tentukan:
- desil ke-1
- desil ke-9
Jawab:
| x | f | F kumulatif |
| 41 – 4546 – 50
51 – 55 56 – 60 61 – 65 |
36
16 8 7 |
39
25 33 40 |
Untuk data kelompok, nilai desil ke-i dari data bergolong dirumuskan sebagai berikut:
Keterangan:
D = desil ke-i
n = banyak data
F = frekuensi kumulatif kelas sebelum kelas desil
f = frekuensi kelas desil
b = tepi bawah kelas
l = lebar kelas
Jadi, desil ke-1 yaitu 46,33 dan desil ke-9 yaitu 62,63.
C. Persentil
- Data Tunggal
Diketahui: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5, tentukan persentil ke-30 dan persentil ke-75.
Jawab:
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
Letak persentil dirumuskan dengan:
Keterangan:
Pi = persentil ke-i
i = 1, 2, 3, . . ., 99
n = banyaknya data
Jadi, persentil ke-30 yaitu 5,3 dan persentilo ke-75 yaitu 9,25.
- Data Kelompok
Diketahui data pada tabel data kelompok di bawah.
| x | f |
| 41 – 4546 – 50
51 – 55 56 – 60 61 – 65 |
36
16 8 7 |
Dari data tersebut tentukan:
- Persentil ke-25
- Persentil ke-60
Jawab:
| x | f | F kumulatif |
| 41 – 4546 – 50
51 – 55 56 – 60 61 – 65 |
36
16 8 7 |
39
25 33 40 |
Nilai persentil ke-i dari data bergolong dirumuskan sebagai berikut.
Keterangan:
Pi = persentil ke-i
b = tepi bawah
n = banyaknya data
F = frekuensi kumulatif kelas sebelum kelas persentil
f = frekuensi kelas persentil
l = lebar kelas
Jadi, persentil ke-25 dari data tersebut yaitu 50,81 dan persentil ke-90 dari data tersebut yaitu 54,825.
Demikianlah pembahasan lengkapnya semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan kalian semua, terima kasih banyak atas kunjungannya. 🙂 🙂 🙂