Pengertian Volume
Volume Tabung – Rumus, Contoh, Luas Dan Cara Menghitungnya – DosenPendidikan.Com– Volume adalah isi dari benda itu. Yang dalam sistem CGS mempunyai satuan cm3 dan dalam MKS mempunyai satuan m3.
Perbedaan Massa dengan Berat
Massa
Massa sebuah benda merupakan banyaknya zat yang terkandung di dalam sebuah benda tersebut. Satuan massa di dalam sistem satuan SI adalah kilogram. Sebagai standar untuk kilogram ini, dibuatlah kilogram standar, yaitu sebuah silinder logam yang terbuat dari platina-iridium, yang sekarang ini disimpan di Sevres, dekat kota Paris. Pada awalnya satu kilogram sama dengan massa dari 1000 cm³ air murni pada suhu dimana kerapatannya maksimum, yaitu 4º C.
Baca Juga : Volume Bola
Berat
Berat adalah besarnya gaya yang dialami benda akibat gaya tarik bumi pada benda tersebut. Untuk keperluan sehari-hari, pencampuradukan pengertian tersebut tidak menjadi masalah, namun dalam fisika atau ilmu pengetahuan eksak, definisi massa dan berat harus benar-benar dibedakan. Massa dan berat memiliki satuan yang berbeda, massa memiliki satuan kilogram, sedangkan berat memiliki satuan Newton.
- Perhatikan tabel berikut.
Luas Permukaan Dan Volume Tabung
Luas Permukaan Tabung
Untuk mencari luas permukaan tabung dapat menggunakan jaring-jaring tabung. Jaring-jaring tersebut terdiri dari :
Baca Juga : “Listrik Dinamis” Pengertian & ( Rumus – Contoh )
- Selimut tabung yang berupa persegi panjang dengan panjang = keliling alas tabung = 2πr dan lebar = tinggi tabung = t, Luas = 2πrt.
- Dua buah lingkaran (alas dan tutup) berjari-jari r. Luas =2πr²
Dengan demikian, luas selimut tabung dapat ditentukan dengan cara berikut :
Luas selimut tabung = keliling alas (p) x tinggi tabung (l)
= 2πr x t
= 2πrt
Luas alas dan tutup tabung = πr² + πr² = 2πr²
Luas permukaan tabung =Luas alas + tutup + luas selimut tabung
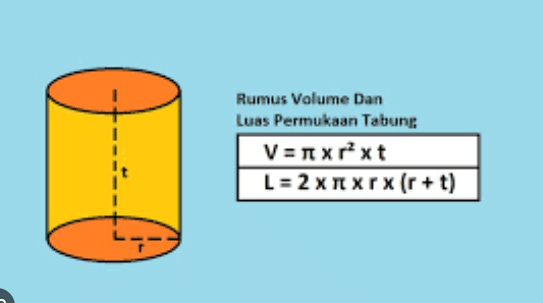
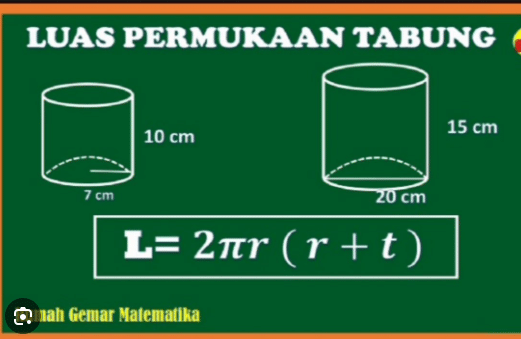
Luas permukaan tabung = 2πr²+2πrt = 2πr(r+t)
Contoh soal :
Sebuah tabung memiliki tinggi 25 cm dan jari-jari alas tabung 14 cm, tentukan luas permukaan tabung !
- Pembahasan :
Diketahui tinggi tabung 25 cm dan jari-jari alas tabung 14 cm
Luas permukaan tabung = 2πr(r+t)
Baca Juga : Rumus Cermin Cembung
Volume Tabung
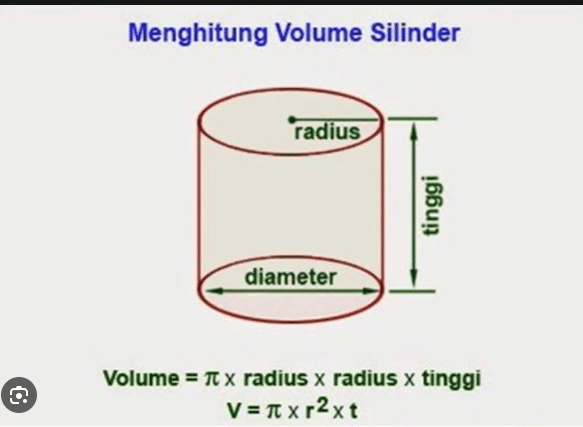
Rumus volume tabung sama dengan luas alas dikalikan tinggi. Karena tabung memiliki alas berupa lingkaran maka volume tabung sama dengan luas alas lingkaran dikalikan tinggi. Sehingga rumus volume tabung adalah sebagai berikut :
Volume Tabung = πr²t
Contoh soal :
Diketahui tabung dengan jari-jari 7 cm dan tingginya 30 cm.Tentukan volume tabung !
- Jawab:
Diketahui tinggi = 20 cm dan jari-jari tabung = 7 cm
Volume tabung = πr²t
Rumus Mencari Volume Tabung
Contoh soal :
Ibu membuat kue keju yang berbentuk tabung untuk persiapan hari raya. Jika jari-jari kue adalah 10 cm dan tingginya 5 cm, berapa volume kue tersebut?
Jawab :
V = 102 5 = 1.570
Jadi, volume kue tersebut adalah 1.570 cm3.
Baca Juga : Lensa Cekung – Pengertian, Sifat, Rumus, Sinar Istimewa dan Contoh
Contoh Soal :
- Hitunglah volume tabung dibawah
Alternati Penyelesaian :
Diketahui : Jari-jari tabung = 2 m
Tinggi tabung = 6 m
Ditanya : Volume tabung.
Penyelesaian :
Jadi, Volume tabungadalah
- Hitung tinggi tabung di bawah
Alternatif Penyelesaian:
Diketahui : diameter = 10 cm, jari-jari = 5 cm
Volume = .
Ditanya :tinggitabung
Penyelesaian :
Jadi, tinggi tabung adalah 12 cm.
- -jari tabung di bawah
Alternatif Penyelesaian :
Diketahui : Volume tabung =
Tinggi tabung = 10 m
Ditanya : jari-jari tabung.
Penyelesaian :
Sekian penjabaran artikel tentang Volume Tabung – Rumus, Contoh, Luas Dan Cara Menghitungnya semoga bermanfaat bagi semua pembaca setia DosenPendidikan.Com