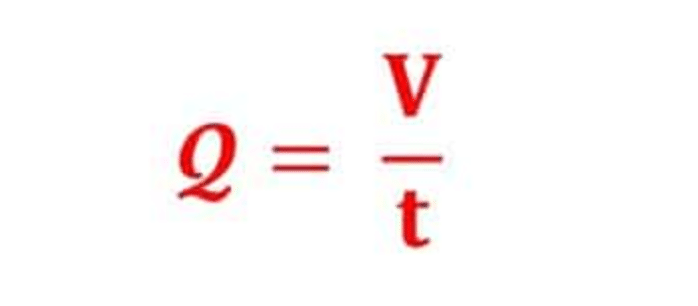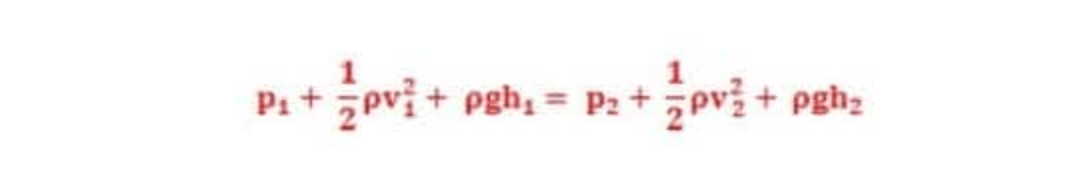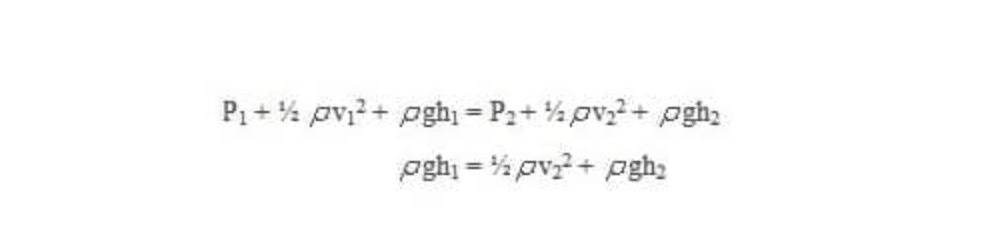Suatu zat yang mempunyai kemampuan mengalir dinamakan Fluida. Cairan adalah salah satu jenis fluida yang mempunyai kerapatan mendekati zat padat. Letak partikelnya lebih merenggang karena gaya interaksi antar partikelnya lemah. Gas juga merupakan fluida yang interaksi antar partikelnya sangat lemah sehingga diabaikan.
fluida dapat ditinjau sebagai sistem partikel dan kita dapat menelaah sifatnya dengan menggunakan konsep mekanika partikel. Apabila fluida mengalami gaya geser maka akan siap untuk mengalir. Jika kita mengamati fluida dinamis misalnya pada semprotan parfum. Berdasarkan uraian diatas, maka pada makalah ini akan dibahas mengenai fluida dinamis.
Pengertian Fluida Dinamis
Fluida dinamis adalah fluida (bisa berupa zat cair, gas) yang bergerak. Untuk memudahkan dalam mempelajari, fluida disini dianggap steady (mempunyai kecepatan yang konstan terhadap waktu), tak termampatkan (tidak mengalami perubahan volume), tidak kental, tidak turbulen (tidak mengalami putaran-putaran).Dalam kehidupan sehari-hari, banyak sekali hal yang berkaitan dengan fluida dinamis ini.
Ciri-Ciri Fluida Dinamis
Berikut ini terdapat beberapa ciri-ciri fluida dinamis, terdiri atas:
- Alirannya tunak (steady), yaitu kecepatan setiap partikel fluida pada satu titik tertentu adalah tetap, baik besar maupun arahnya. Aliran tunak terjadi pada aliran yang pelan.
- Alirannya tak rasional, artinya pada setiap titik partikel fluida tidak memiliki momentum sudut terhadap titik tersebut. Alirannya mengikuti garis arus (streamline).
- Tidak komprisibel (tidak termampatkan), artinya fluida tidak mengalami perubahan volume (massa jenis) karena pengaruh tekanan.
- Tak kental, artinya tidak mengalami gesekan baik dengan lapisan fluida disekitarnya maupun dengan dinding tempat yang dilaluinya. Kekentalan pada aliran fluida berkaitan dengan viskositas.
Jenis-Jenis Fluida Dinamis
Berikut ini terdapat beberapa jenis-jenis fluida dinamis, terdiri atas:
- Aliran lurus atau laminer, yaitu aliran fluida mulus. Lapisan-lapisan yang bersebelahan meluncur satu sama laindengan mulus. Pada aliran partikel fluida mengikuti lintasan yang mulus dan lintasan ini tidak saling bersilangan. Aliran laminer dijumpai pada air yang dialirkan melalui pipa atau selang.
- Aliran turbulen, yaitu aliran yang ditandai dengan adamnya lingkaran-lingkaran tak menentu dan menyerupai pusaran. Aliran turbulen sering dijumpai disungai-sungai dan selokan-selokan.
Besaran-Besaran Fluida Dinamis
Berikut ini terdapat beberapa besaran-besaran fluida dinamis, terdiri atas:
-
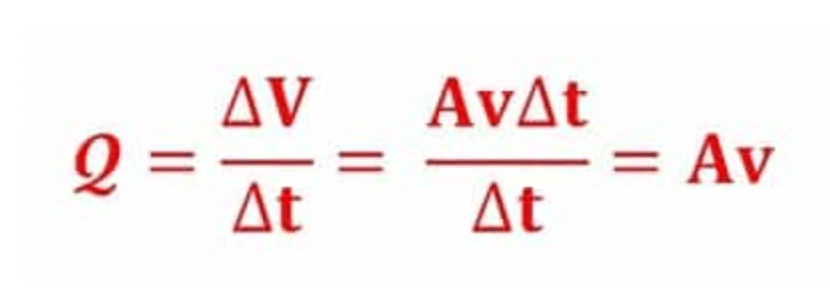
Debit Aliran (Q)
Jumlah volume fluida yang mengalir persatuan waktu, atau:
Keterangan:
Q = debit aliran (m3/s)
A = luas penampang (m2)
V = laju aliran fluida (m/s)
Aliran fluida sering dinyatakan dalam debit aliran
Keterangan:
Q = debit aliran (m3/s)
V = volume (m3)
t = selang waktu (s)
-
Persamaan Kontinuitas
Persamaaan kontinuitas adalah persamaan yang menghubungkan kecepatan fluida dalam dari suatu tempat ke tempat lain. Air yang mengalir di dalam pipa air dianggap mempunyai debit yang sama di sembarang titik.
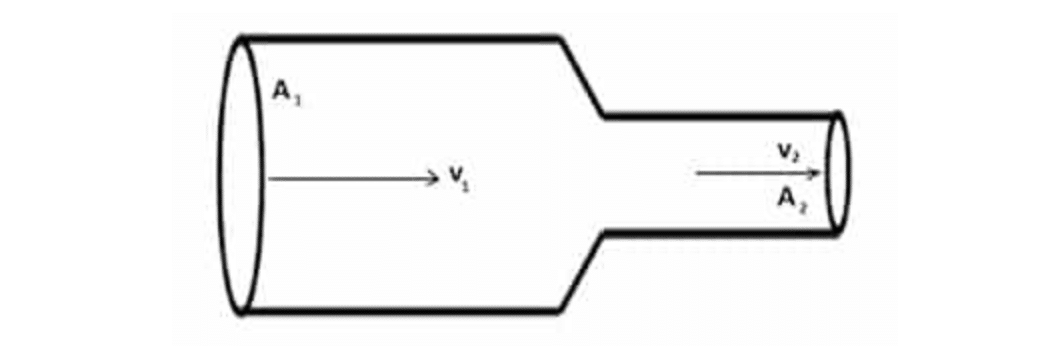
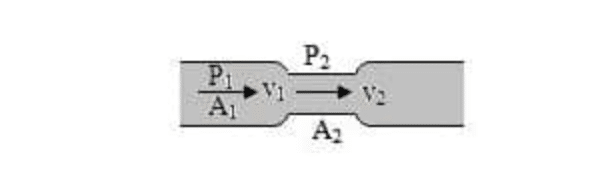
Perhatikan fluida yang mengalir dalam sebuah pipa yang mempunyai ukuran penampang berbeda.
Pipa terletak mendatar dengan ukuran simetris. Partikel fluida yang semula di A1 setelah Dt berada di A2. Karena Dt kecil dan alirannya stasioner maka banyaknya fluida yang mengalir di tiap tempat dalam waktu yang sama harus sama pula.
Banyaknya fluida yang mengalir di A1 sama dengan banyaknya fluida yang mengalir di A2 karena mengikuti kekekalam massa.
massa di A1 = massa di A2
r.A1v1 ∆t = r.A2v2 ∆t
A1v1 = A2v2
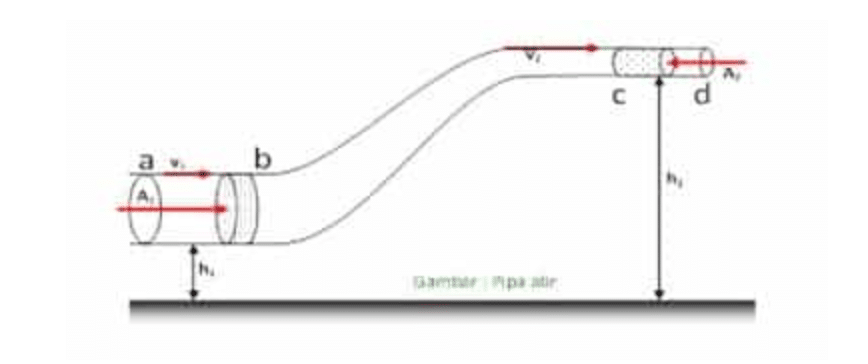
Bagaimana dengan pipa yang memiliki penampang berbeda dan terletak pada ketinggian yang berbeda. Perhatikan tabung alir a-c di bawah ini. A1 adalah penampang lintang tabung alir di a. A2 = penampang lintang di c. v1 = kecepatan alir fluida di a, v2 = kecepatan alir fluida di c.
Air yang mengalir di dalam pipa air dianggap mempunyai debit yang sama di sembarang titik. Atau jika ditinjau 2 tempat, maka:
Debit aliran 1 = Debit aliran 2
Hukum Bernoulli
Hukum Bernoulli adalah hukum yang berlandaskan pada hukum kekekalan energi yang dialami oleh aliran fluida. Hukum ini menyatakan bahwa jumlah tekanan (p), energi kinetik per satuan volume, dan energi potensial per satuan volume memiliki nilai yang sama pada setiap titik sepanjang suatu garis arus. Jika dinyatakan dalam persamaan menjadi :
Keterangan:
p = tekanan air (Pa)
v = kecepatan air (m/s)
g = percepatan gravitasi
h = ketinggian air
Dalam hal ini berlaku Hukum Bernoulli yang menyatakan bahwa jumlah dari tekanan (p), energi kinetik per satuan volum ( ½rv2) dan energi potensial per satuan volum (rgh) memiliki nilai yang sama pada setiap titik sepanjang suatu garis arus.
p1 + ½ rv12 + rgh1 = p2 + ½ rv22 + rgh2
atau p + ½ r v2 + r g h = Konstan
Persamaan tersebut dikenal sebagai hukum Bernoulli.
Dalam hal fluida tak bergerak (statis), v1 = v2 = 0, persamaan Bernoulli diturunkan menjadi :
p1 + ½ r 02 + r g h1 = p2 + ½ r 02 + r g h2
p1 – p2 = rg(h2- h1)
Dalam hal fluida mengalir dalam pipa mendatar (horisontal) di mana h1 = h2
p1 – p2 = r (v22- v12)
Penerapan Hukum Bernoulli
- Pesawat Terbang
Gaya angkat pesawat terbang bukan karena mesin, tetapi pesawat bisa terbang karena memanfaatkan hukum bernoulli yang membuat laju aliran udara tepat di bawah sayap, karena laju aliran di atas lebih besar maka mengakibatkan tekanan di atas pesawat lebih kecil daripada tekanan pesawat di bawah. Akibatnya terjadi gaya angkat pesawat dari hasil selisih antara tekanan di atas dan di bawah di kali dengan luas efektif pesawat.
Keterangan:
– ρ = massa jenis udara (kg/m3)
– va= kecepatan aliran udara pada bagian atas pesawat (m/s)
– vb= kecepatan aliran udara pada bagian bawah pesawat (m/s)
– F= Gaya angkat pesawat (N)
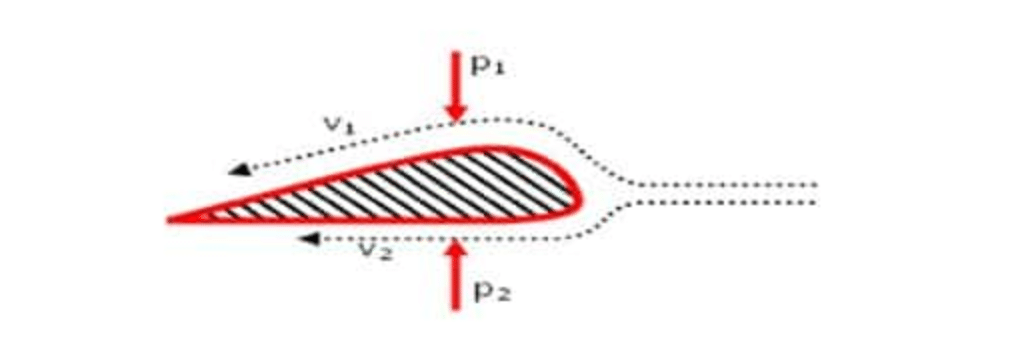
Pembahasan gaya angkat pada sayap pesawat terbang dengan menggunakan persamaan Bernoulli dianggap bentuk sayap pesawat terbang sedemikian rupa sehingga garis arus aliran udara yang melalui sayap adalah tetap (streamline).
Penampang sayap pesawat terbang mempunyai bagian belakang yang lebih tajam dan sisi bagian yang atas lebih melengkung daripada sisi bagian bawahnya. Bentuk ini menyebabkan kecepatan aliran udara di bagian atas lebih besar daripada di bagian bawah (v2 > v1).
Dari persamaan Bernoulli kita dapatkan :
|
Ketinggian kedua sayap dapat dianggap sama (h1 = h2), sehingga
r g h1 = r g h2.
dan persamaan di atas dapat ditulis :
|
Dari persamaan di atas dapat dilihat bahwa v2 > v1 kita dapatkan p1 > p2 untuk luas penampang sayap F1 = p1 A dan F2 = p2 A dan kita dapatkan bahwa F1 > F2. Beda gaya pada bagian bawah dan bagian atas (F1 – F2) menghasilkan gaya angkat pada pesawat terbang. Jadi, gaya angkat pesawat terbang dirumuskan sebagai :
|
Dengan r = massa jenis udara (kg/m3)
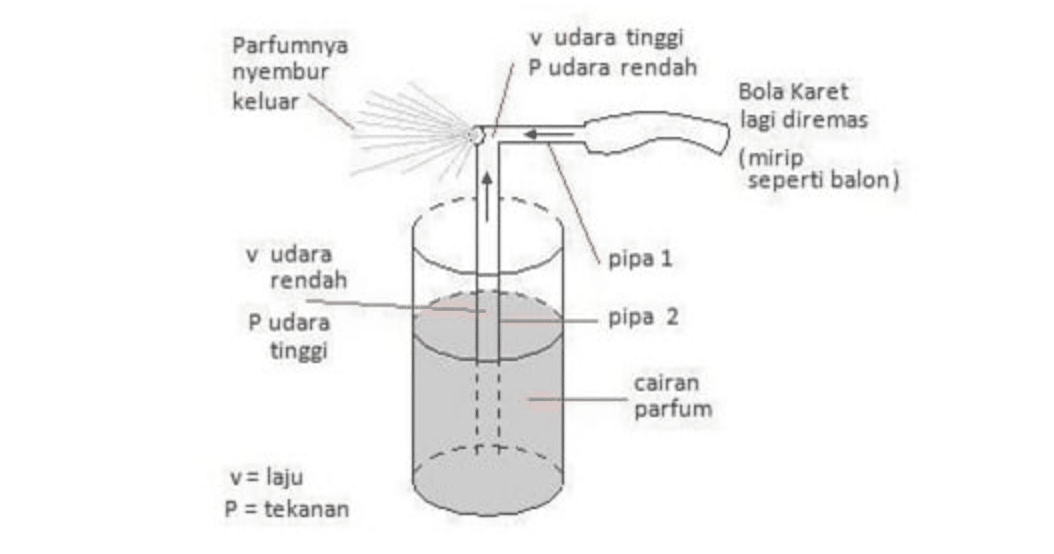
- Penyemprot Parfum dan Obat Nyamuk
Prinsip kerja yang dilakukan dengan menghasilkan laju yang lebih besar pada ujung atas selang botol sehingga membuat tekanan di atas lebih kecil daripada tekanan di bawah. Akibatnya cairan dalam wadah tersebut terdesak ke atas selang dan lama kelamaan akan menyembur keluar.
- Teorema Toricelli (laju effluk)
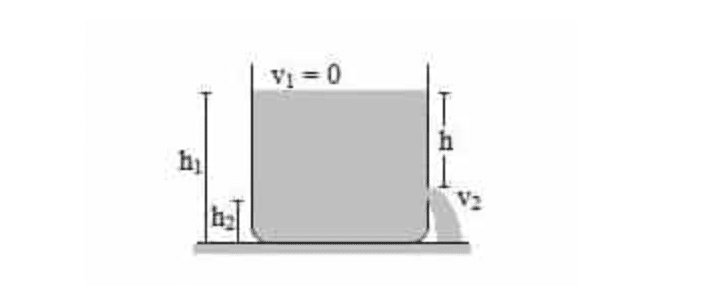
Kita terapkan persamaan Bernoulli pada titik 1 (permukaan wadah) dan titik 2 (permukaan lubang). Karena diameter kran/lubang pada dasar wadah jauh lebih kecil dari diameter wadah, maka kecepatan zat cair di permukaan wadah dianggap nol (v1 = 0). Permukaan wadah dan permukaan lubang/kran terbuka sehingga tekanannya sama dengan tekanan atmosfir (P1 = P2). Dengan demikian, persamaan Bernoulli untuk kasus ini adalah :
Berdasarkan persamaan ini, tampak bahwa laju aliran air pada lubang yang berjarak h dari permukaan wadah sama dengan laju aliran air yang jatuh bebas sejauh h (bandingkan Gerak jatuh Bebas).
- Efek Venturi
Selain teorema Torricelli, persamaan Bernoulli juga bisa diterapkan pada kasus khusus lain yakni ketika fluida mengalir dalam bagian pipa yang ketinggiannya hampir sama (perbedaan ketinggian kecil). Untuk memahami penjelasan ini, amati gambar di bawah.
Pada gambar di atas tampak bahwa ketinggian pipa, baik bagian pipa yang penampangnya besar maupun bagian pipa yang penampangnya kecil, hampir sama sehingga diangap ketinggian alias h sama. Jika diterapkan pada kasus ini, maka persamaan Bernoulli berubah menjadi :
Ketika fluida melewati bagian pipa yang penampangnya kecil (A2), maka laju fluida bertambah (ingat persamaan kontinuitas). Menurut prinsip Bernoulli, jika kelajuan fluida bertambah, maka tekanan fluida tersebut menjadi kecil. Jadi tekanan fluida di bagian pipa yang sempit lebih kecil tetapi laju aliran fluida lebih besar.
Ini dikenal dengan julukan efek Venturi dan menujukkan secara kuantitatif bahwa jika laju aliran fluida tinggi, maka tekanan fluida menjadi kecil. Demikian pula sebaliknya, jika laju aliran fluida rendah maka tekanan fluida menjadi besar.
Contoh Soal Fluida Dinamis
Soal 1
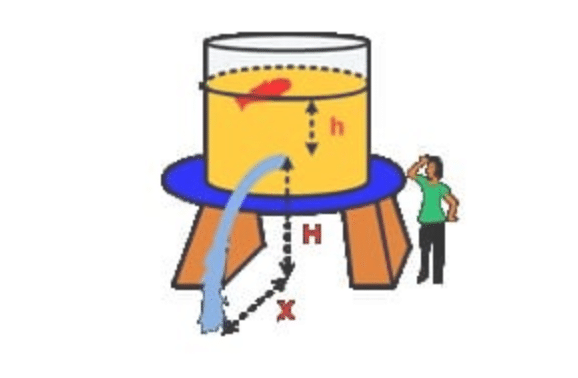
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!
Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan :
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Pembahasan
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon
Soal 2
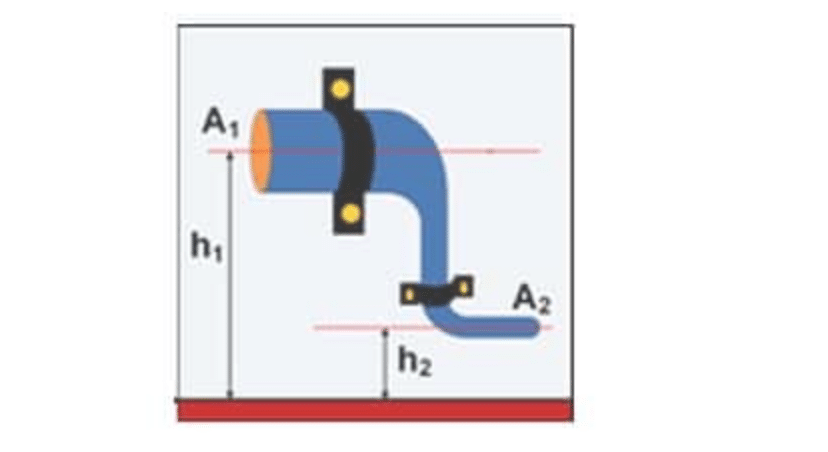
Pipa untuk menyalurkan air menempel pada sebuah dinding rumah seperti terlihat pada gambar berikut! Perbandingan luas penampang pipa besar dan pipa kecil adalah 4 : 1.
Posisi pipa besar adalah 5 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 36 km/jam dengan tekanan 9,1 x 105 Pa. Tentukan :
a) Kecepatan air pada pipa kecil
b) Selisih tekanan pada kedua pipa
c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)
Pembahasan
Data :
h1 = 5 m
h2 = 1 m
v1 = 36 km/jam = 10 m/s
P1 = 9,1 x 105 Pa
A1 : A2 = 4 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(4)(10) = (1)(v2)
v2 = 40 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(402 − 102) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa
−V12)
P1 − P2 = 1/2(1000)(402 − 102) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa
P1 − P2 = 1/2(1000)(402 − 102) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa
)2) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)((40)2 − (10)2) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa
Soal 3
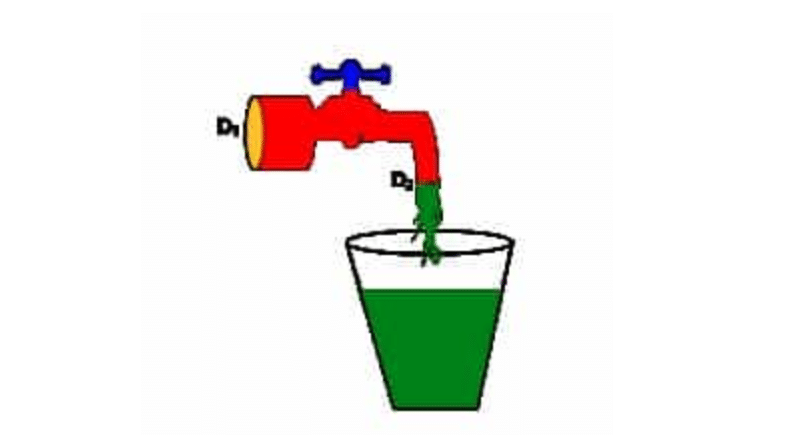
Ahmad mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran seperti gambar berikut!
Jika luas penampang kran dengan diameter D2 adalah 2 cm2 dan kecepatan aliran air di kran adalah 10 m/s tentukan:
a) Debit air
b) Waktu yang diperlukan untuk mengisi ember
Pembahasan
Data :
A2 = 2 cm2 = 2 x 10−4 m2
v2 = 10 m/s
a) Debit air
Q = A2v2 = (2 x 10−4)(10)
Q = 2 x 10−3 m3/s
b) Waktu yang diperlukan untuk mengisi ember
Data :
V = 20 liter = 20 x 10−3 m3
Q = 2 x 10−3 m3/s
t = V / Q
t = ( 20 x 10−3 m3)/(2 x 10−3 m3/s )
t = 10 sekon
Demikianlah pembahasan mengenai Fluida Dinamis – Pengertian, Ciri, Jenis, Besaran, Rumus, Penerapan dan Contoh Soal semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua, terima kasih banyak atas kunjungannya.